- 声学楼论坛 (http://nju520.com/bbs/index.asp)
-- 基础理论室 (http://nju520.com/bbs/list.asp?boardid=17)
---- 傅里叶变换(Transformée de Fourier) (http://nju520.com/bbs/dispbbs.asp?boardid=17&id=7360)
-- 发布时间:2007-3-16 1:46:02
-- 傅里叶变换(Transformée de Fourier)
http://zh.wikipedia.org/wiki/%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2#.E6.A6.82.E8.A6.81.E4.BB.8B.E7.BB.8D
傅里叶变换
维基百科,自由的百科全书
| 下载信息 [文件大小: 下载次数: ] | |
 点击浏览该文件: 点击浏览该文件: |
-- 发布时间:2007-3-16 1:50:45
--
公式是丢掉了.
以后再说.
有一个词叫
快速傅里叶变换.
英文缩写为FFT.
这个FFT在好几个计算机测试系统上是有的.
-- 发布时间:2007-3-16 3:28:09
--
在下是新手。敢问这里又没做数字信号及心理学对声学信号处理的 (psychoacoustic)?
对于有些受先天条件限制而硬件不科技的升学设计,此法可谓毕经之道。不知哪位高手可知道那些这方面的权威书可否共享?
-- 发布时间:2007-3-16 4:42:26
--
http://www.nju520.com/bbs/dispbbs.asp?boardID=10&ID=1644&page=1
试试吧.
-- 发布时间:2007-3-16 8:51:36
--
谢谢老兵了,好资料。
-- 发布时间:2007-3-17 0:23:43
--
谢谢老兵了,好资料。
谢谢,希望能把这个帖子搞成个好帖子.
-- 发布时间:2007-3-17 0:28:42
--
Fourier级数的概念是在高等数学内的,
Fourier变换的概念在我的大学期间是放在数学物理方程这个课程中的,
可以说都在数学里,拿到这儿说的目的就是想让大家来讨论
频率分析的有关问题.
-- 发布时间:2007-3-17 0:40:02
--
问题1:
连续的有重复性的声波波形在时间轴上如果是没有结尾的话,
如果对它的波形进行傅氏分析的话,那结果就是
一串正弦波的叠加,是基频F,2F和3F等的正弦波,它们的幅度是不一样的,还可能带不同的相角.
那末,其数学表达式是什么呢?
-- 发布时间:2007-3-17 1:10:48
--
还是接着上面这个问题,
这个波形在时间轴上是连续的,
但是要表现它的频谱的话,就是横轴是频率的话,
画出这个波形的频谱的话,那就是一条条的直线,
每条线的高度对应于某个频率分量的大小.
总体上,这是个谱线有间隔的频谱图.
跟据这个频谱图,能不能确定那个原来的周期波形呢?
以上是根据记忆写下来的,个别字眼恐怕是不够严格的,
那么,就请有心人补上更严格的说法和相关的图例了,
没图是很难理解正确的了.
-- 发布时间:2007-3-18 1:07:20
--
第二个问题是实际的了.
就是COOL EDIT 软件的使用中的关于频率分析的应用.
一段音乐或语音信号,它的频谱是怎样的呢?
好,在COOL EDIT 软件上有个功能是能做的,
怎样做呢?
它是用的什么数学理论呢?
我想大家对这一问是答得上来的吧,
但是要向细处问和深处问,哈哈,问题多多了啊.
本楼的测试板块上有过COOL EDIT软件的介绍的啦.
-- 发布时间:2007-3-18 3:31:00
--
在COOL EDIT 软件上有个功能是能做的,
怎样做呢?
最好是试用那个软件,再对某段音乐作频率分析,
看看那段音乐的频谱特征,
然后要试试菜单中提供的选择功能,
......
-- 发布时间:2007-3-20 0:30:04
--
对第一问请参看
http://col.njtu.edu.cn/zskj/5012/sANDs/xuexi/chart3/C_3_2_2.htm
-- 发布时间:2007-3-20 0:34:44
--
请接着看
http://col.njtu.edu.cn/zskj/5012/sANDs/xuexi/chart3/C_3_2_2_2.htm
-- 发布时间:2007-3-20 0:41:15
--
设周期函数
![]()
的周期为
![]()
,角频率
![]()
,其三角形式傅立叶级数为
![]()
式中系数
![]()
称为傅立叶级数。
![]()
![]()
周期信号傅立叶级数的含义
任何满足狄里赫利条件的周期信号可分解为直流和许多余弦(或正弦)分量。
其中第一项
![]()
为常数项,它是周期信号中所包含的直流分量;式中第二项
![]()
称为基波或一次谐波,它的角频率和原周期信号相同,
![]()
是基波振幅,
![]() 是基波初相角;式中第三项
是基波初相角;式中第三项
![]() 称为二次谐波,它的频率是基波频率的二倍,
称为二次谐波,它的频率是基波频率的二倍,
![]() 是二次谐波振幅,
是二次谐波振幅,
![]() 是其初相角。依次类推,还有三次、四次、……等谐波。一般而言,
是其初相角。依次类推,还有三次、四次、……等谐波。一般而言,
![]() 称为
称为
![]() 次谐波,
次谐波,
![]() 是二次谐波振幅,
是二次谐波振幅,
![]() 是其初相角。
是其初相角。
-- 发布时间:2007-3-20 0:53:30
--
请注意上面的引用又丢了一个式子.
原文中是贴图,我没有贴过来,如有某位网友能据此补充,形成前后符号统一的文章,
我将是无比的欢迎.
如果能将主帖里的丢掉的符号捡回来,就更好了.
-- 发布时间:2007-3-20 0:59:14
--
任何满足狄里赫利条件的周期信号可分解为直流和许多余弦(或正弦)分量。
这句话是回答第一问的关键.
狄里赫利条件是什么?请查一下.
要记住的关键词是周期信号这个词.
那么是不是有"非周期信号"这个词?
对.
-- 发布时间:2007-3-22 5:39:30
--
Fourier Series
If a continuous function f(t) is periodic with period T, then it may be approximated arbitrarily well by a Fourier series
如果一个连续函数f(t)是一个周期为T的周期函数的话,那末它就可相当随意地近似表达为一个傅利叶级数
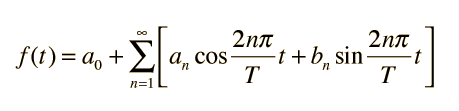
where the coefficients are given by:
其中的系数由下式确定:
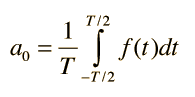
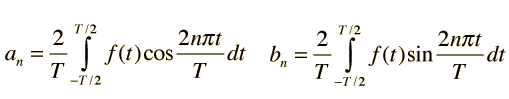
-- 发布时间:2007-3-22 6:25:42
--
还是英文资料里能容易地贴过来公式.
看上面的第1式,可知一个这样的时间函数是表达为级数了,
ao这一项体现了它有直流分量,而西格马符号后表达的是一系列正弦波和余弦波的叠加,
n=1到无穷大是说明在理论上是无限多.
n=1所表达的就是基波,a1,b1代表的是基波的大小,
n=2所表达的就是二次谐波,a2,b2代表的是二次谐波的大小
n=3所表达的就是三次谐波,a3,b3代表的是三次谐波的大小
其余的n,类推.
这样,一个波形再复杂的波,只要它是连续的周期波,就能将其分解成基波和各次谐波的叠加,
而且各个谐波的大小是求得出来的.
这样一个连续的有周期的信号是一个理论上的存在吗?
不仅仅是,
一个正弦信号发生器接功率放大器,然后再接上扬声器,
只要输出达到稳定了,输出频率不变时所产生的声音都可近似地被看成无限的连续的周期信号.
特别是有的信号发生器不仅有正弦波,还有三角波和方波,
在它们输出三角波和方波时,它们的频率成份是怎样的呢
如果掌握了这儿的有关知识,就是很简单的求积分的问题,而有关公式就在上面.
这就是频率分析的数学基础.
-- 发布时间:2007-3-23 1:42:27
--
我在GOOGLE里打入傅里叶级数的英文,选PDF文挡,搜索.
得到的是几十万个有关条目.
说明它是多么重要.
然而下下来一看,又不是很满意,有的是太深奥了,
有的是表达式和上面的不大一致,引完后,对初学者来说容易引起混淆.
还不如慢慢来一点一点加强理解的好.
请注意我这两天的跟帖只是在讲傅里叶级数,还没牵涉到傅里叶变换呢.
傅里叶级数是基础,要首先搞通.
-------
要搞明白的是:
在时间轴上,一个连续的周期性波形,..
这样一个信号在频率轴上的表达成了一条条有间隔的直线了.
这二者之间有对等关系,
有前者,就必然有后者,
而反之亦然,有后者就有前者.
如果在频率轴上,标定上基波,二次谐波,三次谐波,四次..等等的位置,
再用直线的标高表示它们各自的幅度,....
那么,我们就能据此构画出它在时间轴上应该是如何的一个波形了,..
啊,这就是频率合成的最基本的数学原理啊.
电子琴的设计师需要掌握的啊.
-- 发布时间:2007-3-23 9:28:02
--
版筑的这些铁子都是理解频谱分析及数字信号处理的基础。众所周知
完全的周期信号在现实中是没有的,为了方便的对采样到的离散
新号进行数自分析,就采用抽象的周期延拓办法构造完整周期信号
这样我们得到频谱在频域就是一条一条的谱线了