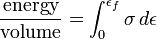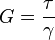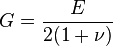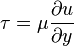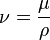标题:杨氏模量以及材料的刚度硬度强度的相关知识
杨氏模数(Young's modulus )是材料力学中的名词,弹性材料承受正向应力时会产生正向应变,定义为正向应力与正向应变的比值。公式记为
其中,E 表示杨氏模数,σ 表示正向应力,ε 表示正向应变。
杨氏模量取决于材料的组成。举例来说,大部分金属在合金成分不同、热处理在加工过程中的应用,其杨氏模量值会有5%或者更大的波动。正如以下的很多材料的杨氏模量值非常接近。
| 材料 | 杨氏模量 (E) in GPa | 杨氏模量 (E) in lbf/in2 |
|---|---|---|
| 橡胶(微小应变) | 0.01-0.1 | 1,500-15,000 |
| 低密度聚乙烯 | 0.2 | 30,000 |
| 聚丙烯 | 1.5-2 | 217,000-290,000 |
| 聚对苯二甲酸乙二酯 | 2-2.5 | 290,000-360,000 |
| 聚苯乙烯 | 3-3.5 | 435,000-505,000 |
| 尼龙 | 2-4 | 290,000-580,000 |
| 橡木(颗粒表面) | 11 | 1,600,000 |
| 高强度混凝土(受到压缩) | 30 | 4,350,000 |
| 金属镁 | 45 | 6,500,000 |
| 玻璃(所有种类) | 10,400,000 | |
| 铝 | 69 | 10,000,000 |
| 黄铜和青铜 | 103-124 | 17,000,000 |
| 钛 (Ti) | 105-120 | 15,000,000-17,500,000 |
| 碳纤维强化塑料(单向,颗粒表面) | 150 | 21,800,000 |
| 合金与钢 | 190-210 | 30,000,000 |
| 钨 (W) | 400-410 | 58,000,000-59,500,000 |
| 碳化硅(SiC) | 450 | 65,000,000 |
| 碳化钨(WC) | 450-650 | 65,000,000-94,000,000 |
| 单碳纳米管 [1] | approx. 1,000 | approx. 145,000,000 |
| 钻石 | 1,050-1,200 | 150,000,000-175,000,000 |
刚度是材料力学中的名词,定义为施力与所产生变形量的比值,表示材料或结构抵抗变形的能力。公式记为
其中k 表示刚度,P 表示施力,δ 表示变形量(变形后的长度减去原长或原长减去变形后的长度)。在国际单位制中,刚度的单位为牛/米。一般应用于胡克定律作系统的振动分析。
将欲检测的材料与一个或多个已知硬度的材料相互刻划,在后者上留下划痕说明硬度≥后者,反之≤后者硬度。这类方法能够通过比较粗略估计硬度,但不够精确。
将特制的压头用一定负荷压入在材料上一段时间,通过测量形成的压痕来确定硬度。硬度高的材料上产生的压痕小。
在材料科学及冶金学上,韧性是指当承受应力时对折断的抵抗,其定义为材料在破裂前所能吸收的能量与体积的比值。
韧性可从在应力-应变曲线之下的面积(用积分)求得,明确的数学描述如下:
其中:
- ε 是应变
- εf 是断裂时的应变
- σ 是应力
另一个定义是直至断裂时能吸收到多少机械能(或动能)的能力。
韧性在国际单位制中是用焦耳每立方米(J/m3)来测量;在英制中是用磅力每平方英寸(有时以in-lbf/in3表达)来测量。
根据外力的作用方式,有多种强度指标,如抗拉强度、抗弯强度、抗剪强度等。当材料承受拉力时,强度性能指标主要是降伏强度和抗拉强度。
注意强度和硬度是本质上不同的概念。玻璃等硬而脆的物质虽然硬度大(变形与外力之比小)但强度小(在断裂之前能承受的总外力小)。对于同系列的金属,此二者可以有一定的对应关系。强度测量往往需要彻底毁坏材料,而硬度试验则毁坏较小或不毁坏。所以校定的硬度强度换算关系被用来由硬度推算强度。
- 金属材料的强度
是金属材料的在外力作用下抵抗永久变形和断裂的能力。工程上常用来表示金属材料强度的指标有屈服强度和抗拉强度。
- 屈服强度
- 屈服强度是金属材料发生屈服现象时的屈服极限,亦即抵抗微量塑性变形的应力。
δS=Fs/AO
Fs----试样产生屈服现象时所承受的最大外力(N)
AO----试样原来的截面积(mm2)
δS---屈服强度(Mpa)
- 抗拉强度
- 抗拉强度是指金属材料在拉断前所能承受的最大应力,用δb=FO/AO
FO----试样在断裂前的最大外力(N)
AO----试样原来的截面积(mm2)
δb---抗拉强度(Mpa)
除简单的力学振动阻尼外,阻尼的具体形式还包括电磁阻尼、介质阻尼、结构阻尼,等等。尽管科学界目前已经提出了许多种阻尼的数学模型,但实际系统中阻尼的物理本质仍极难确定。下面仅以力学上的粘性阻尼模型为例,作一简单的说明。
粘性阻尼可表示为以下式子:
|
Bulk modulus (K) ? Young's modulus (E) ? Lamé's first parameter (λ) ? Shear modulus (G) ? Poisson's ratio (ν) ? P-wave modulus (M) |
| [hide]Conversion formulas | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these, thus given any two, any other of the elastic moduli can be calculated according to these formulas. | ||||||||||
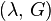 |
 |
 |
 |
 |
 |
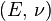 |
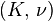 |
 |
 | |
 |
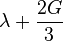 |
 |
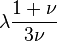 |
 |
 |
 | ||||
 |
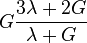 |
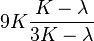 |
 |
 |
 |
 |
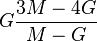 | |||
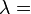 |
 |
 |
 |
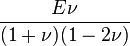 |
 |
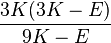 |
 | |||
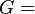 |
 |
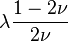 |
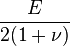 |
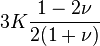 |
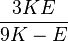 | |||||
 |
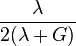 |
 |
 |
 |
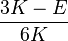 |
 | ||||
 |
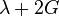 |
 |
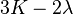 |
 |
 |
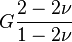 |
 |
 |
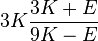 | |
泊松比(英语:Poisson's ratio),又译蒲松比,是材料力学和弹性力学中的名词,定义为材料受拉伸或压缩力时,材料会发生变形,而其横向变形量与纵向变形量的比值,是一无量纲的物理量。
剪切模量G、杨氏模量E 和泊松比ν三个量中只有两个是独立的,它们之间存在以下关系:

剪力模数(shear modulus )是材料力学中的名词,弹性材料承受剪应力时会产生剪应变,定义为剪应力与剪应变的比值。公式记为
其中,G 表示剪力模数,τ 表示剪应力,γ 表示剪应变。在均质且等向性的材料中:
固体力学是力学中研究固体机械性质的学科,连续介质力学组成部分之一,主要研究固体介质在外力,温度和形变的作用下的表现,是连续介质力学的一个分支。一般包括材料力学、弹性力学、塑性力学等部分。固体力学广泛的应用张量来描述应力,应变和它们之间的关系。
在固体力学中,线性材料模型的应用是最为广泛的,但是很多材料是具有非线性特性的,随着新材料的应用和原有材料达到它们应用的极限,非线性模型的应用愈加广泛。
1. 弹性- 当应力被移除后,材料恢复到变形前的状态。线性弹性材料的形变与外加的载荷成正比,此关系可以用线性弹性方程,例如胡克定律,表示出来。
2. 黏弹性- 材料不仅具有弹性,而且具有摩擦。当应力被移除后,一部分功被用于摩擦效应而被转化成热能,这一过程可用应力应变曲线表示。
3. 塑性- 如果施加的应力小于实际的结果,材料便呈现塑性,不能恢复到初始状态。也就是说屈服之后的形变是永久性的。
粘性,又称黏度、黏滞系数,是流体力学的专有名词,是度量流体随剪应力或外部应力而形变时,流体抵抗形变的阻力,也可以表示流体内部的摩擦力大小。
黏度 μ 定义为流体承受剪应力时,剪应力与剪应变梯度(剪应变随位置的变化率)的比值,数学表述为:
式中:τ为剪应力,u为速度场在x方向的分量,y为与x垂直的方向坐标。
黏度较高的物质,比较不容易流动;而黏度较低的物质,比较容易流动。例如油的黏度较高,因此不容易流动;而水黏度较低,不但容易流动,倒水时还会出现水花,倒油时就不会出现类似的现象。
动黏滞系数 ν 是将黏滞系数 μ 除以流体密度 ρ:
| |||||||
|
水仙超版辛苦了
学习了,谢谢!