标题:最佳传输线音箱研究里的一个可疑问题...
《最佳传输线音箱研究》,算是一篇专业文章了,还是翻译的老外作品。
但是,在对常见的传输线音箱(就是文章里说的C型系统)的论证,是不是可疑?
为此,摘录原文如下:
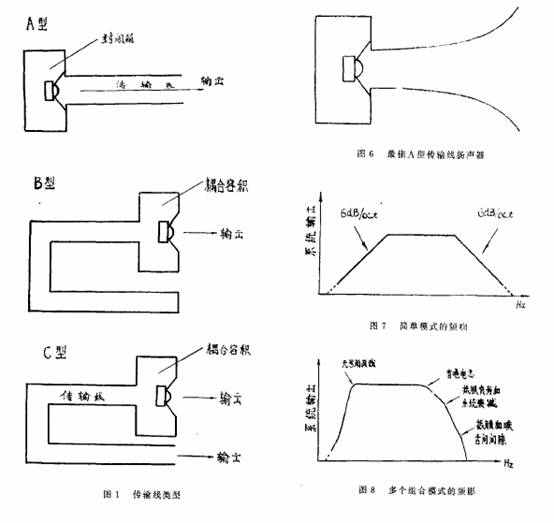
对 于 C型 系统,正 如在 开 口箱 的直接辐射 系统中一 样,相 当于增加 了一个输 出源,传输管的喉部 阻抗 ,也 随频率而变,由于管的末 端开 口,所 以其声阻抗比较低 ;与电路短 路相 似,这与 B型 系统 相反。其反射 系数实质是+1,当管子是1/4声波波长 的奇次 倍时,则对辐射器呈 现高的声 阻 抗,大部分输出传 到管子,若管子是半波 长的 奇数倍时辐射器输出与管 口输出相位相同。若辐射器与管口挨得很近,则结果是 相 加 的。
若管长是波长的整数倍,则输出相 反,相 互 抵消。这样在 频响曲线上 又 出现峰谷。
是这样的吗?
请各位帮忙看看了。
 此主题相关图片如下:4.12传输线绿咪对低金黄倒相咪对低音红耦合叠加咪对气孔.jpg
此主题相关图片如下:4.12传输线绿咪对低金黄倒相咪对低音红耦合叠加咪对气孔.jpg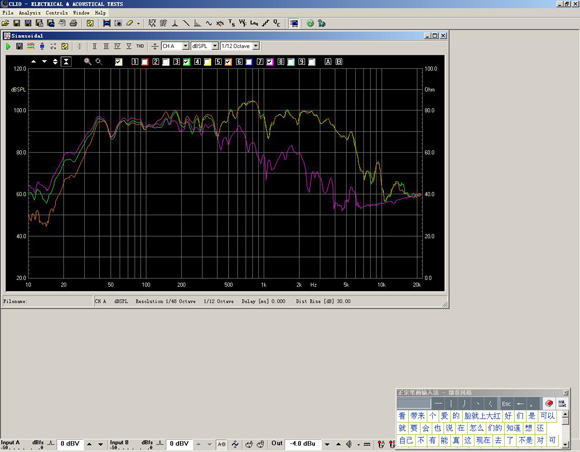
 此主题相关图片如下:f 006.jpg
此主题相关图片如下:f 006.jpg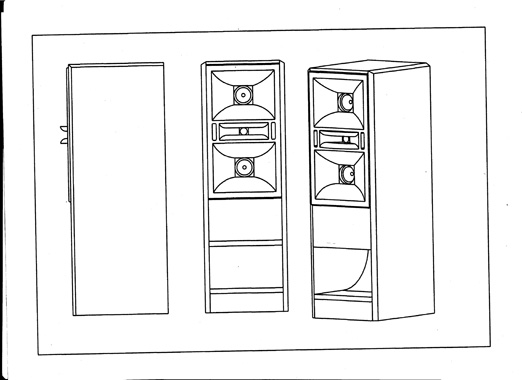
关于传输线音箱,我的理解是一个倒相式音箱为了扩展低频从而增加体积,为了防止箱体共振频率太低,从而加一些隔板,最后出来的就是传说中的 传输线音箱。
不愧是“玛田音箱”,很有自己的理念。
有的时候,我们希望音箱的体积尽可能小。但这不是最终的目的。
传输线音箱就可以在同样的单元的情况下采用更大的体积(因为很多时候体积并不都是瓶颈或约束条件),而倒相箱就无能为力的。你增加了体积(指在正确的设计的参数后)可能的结果是低频的表现更差。
所以,可以采用更大的体积在一定条件下也是一个优势。
为什么不是呢?
至于老兄说的是为了什么什么而增加隔板,从而变出一个传输线音箱,也是可能的一个想法。只是不知道历史上是不是这样?
在一个新的东西没有产生前,是没有什么理论可以指导的,也许就是这样隔来隔去而意外得到什么好结果的。
当然,我们不是音箱史的编写者,也不会去较劲到底是怎样把传输线变成了的吧?
谢谢关注了。
路过!求学!
反射 系数实质是+1,【对于我们欲观察的低频来说,近似在管道无损失,所以说它反射系数为1】
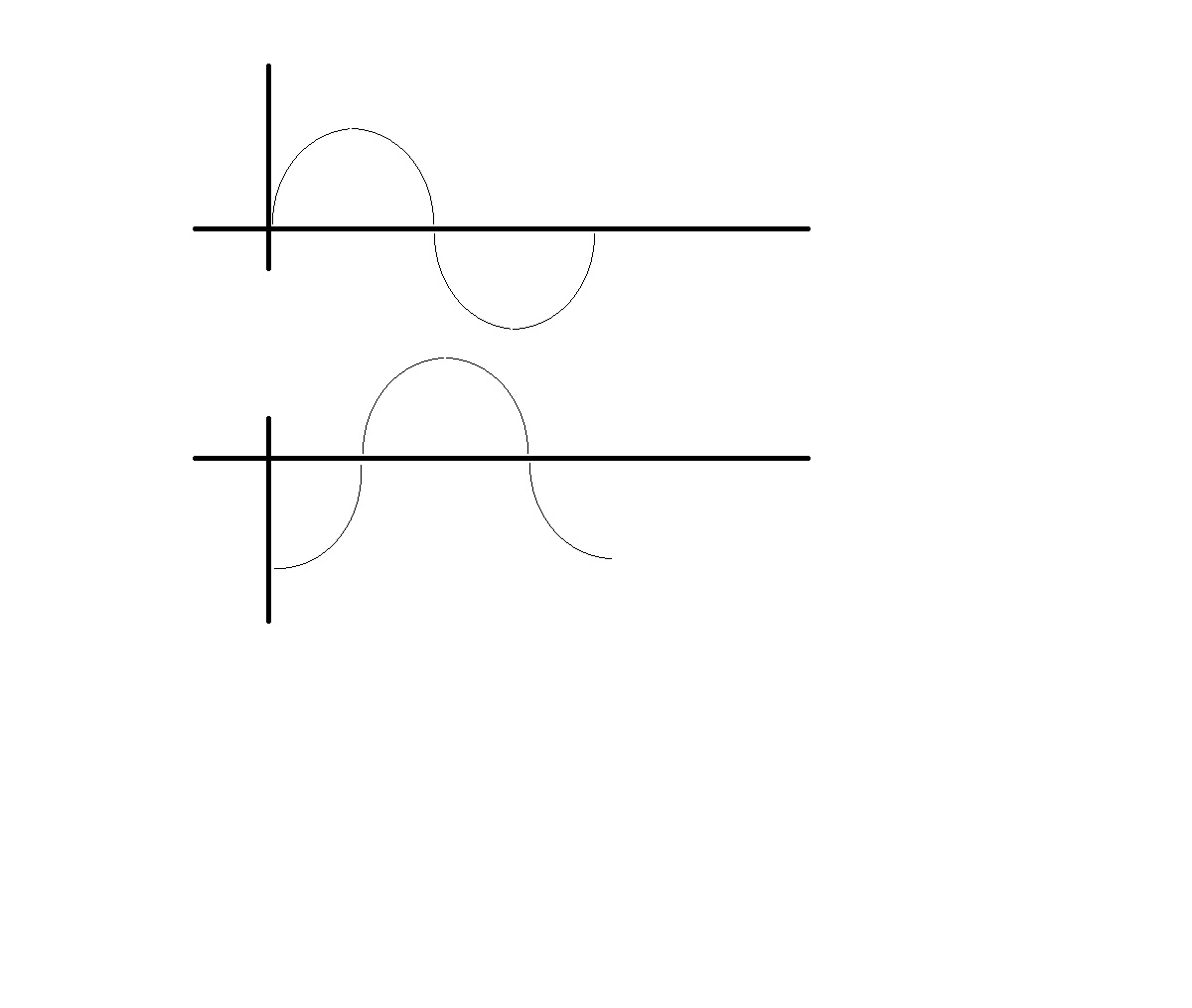
当管子是1/4声波波长 的奇次 倍时,则对辐射器呈 现高的声 阻 抗,大部分输出传 到管子,【如我附件图,一个是正面辐射声波,另一个则是相对应从纸盆反面发出,经管道相位延迟90或270度后的声波。两者叠加后,为高阻抗状态。但还不是最高阻抗】
若管子是半波 长的 奇数倍时辐射器输出与管 口输出相位相同。若辐射器与管口挨得很近,则结果是 相 加 的。【纸盆反面的声波与正面声波差180度,再经管道倒相180度,则相位一致了。所以会有叠加的结果】
若管长是波长的整数倍,则输出相 反,相 互 抵消。这样在 频响曲线上 又 出现峰谷。【最高阻抗状态】
楼顶的红字论述是对的,不加吸音的C型频响常易出现峰谷。
 此主题相关图片如下:d 007-1.jpg
此主题相关图片如下:d 007-1.jpg
(若管子是半波 长的 奇数倍时辐射器输出与管 口输出相位相同。若辐射器与管口挨得很近,则结果是 相 加 的。【纸盆反面的声波与正面声波差180度,再经管道倒相180度,则相位一致了。所以会有叠加的结果】
若管长是波长的整数倍,则输出相 反,相 互 抵消。这样在 频响曲线上 又 出现峰谷。【最高阻抗状态】) 你好,箱子的设计基本上根据就是你上面所说 的理论,箱子共分耦合腔,收窄声导管,前后声波叠加腔,前声波中频吸收腔组成,低频自然衰减至300HZ以下,以同一相位输出,中高频是预留独立腔体,可衔接任何设计的中高音. 以上设计巳申请专利,是否合适,还望指教,谢谢.
对波长远大于管径的声波,管任一截面的声阻抗可以写成:Z[x]=Zr*Tanh[a+I k x],Zr为参考阻抗;
管前端:Z[-L]=Zr*Tanh[a-I k L];
出口:Z[0]=Zr*Tanh[a];
对刚性壁:Z[0]=∞,a=I Pi/2;Z[-L]=Tanh[I Pi/2-I k L]=I cot[k L]。
当KL为Pi/2的整数倍时,Z[-L]=0,意味着该处出现共振,能较强烈的吸收声,当然此模型
初始假设已不成立。
当KL为Pi的整数倍时,依旧可看成刚性壁,基本没影响。
对自由辐射出口:Z[0]=Zr*Tanh[a],a一般都很小,a<<1,与波长比可近似为零。
Z[-L]=Zr*Tanh[a-I k L]=-Zr*I Tan[ (I a+k L)],
当KL=Pi/2,即1/4波长管,Z[-L]=Zr* Cot[a]≈∞,相当于刚性壁,虽然此时在管前端的声压
比较大,但实际的声体积速度却很小,辐射效率不一定会增加。这里想要辐射效率
增加,更关键的还是需要做到与前端阻抗匹配,当然这里如果后腔足够大,以 致腔
体阻抗比输入阻抗要小,该方法可以增加辐射。
当kL=Pi,即1/2波长管,Z[-L]=Zr*Tanh[a],相当于直接辐射。
学习了!
楼上说的可不是一般人都知道的或肯来这里说的了,谢谢!
chaogo兄可以很好的参考,理论方面的加强是“实践派”提升的一条必经之道。
请楼上的多指点了,谢谢!
 此主题相关图片如下:cimg8624.jpg
此主题相关图片如下:cimg8624.jpg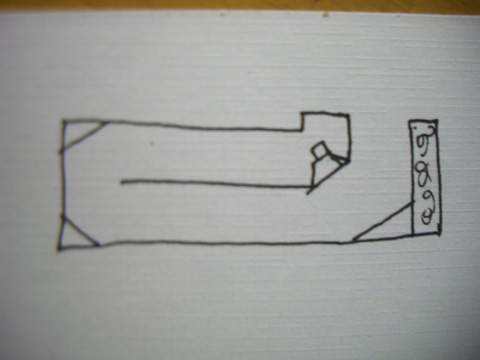
感情楼上各位的详细指导,正在结合以上的论述对箱内结构作进一步推敲和改进,因理论差,还想进一步请教:一.喇叭前后声波在箱内叠加的反射角度,形式和相位的关系,二.假设管道长从2Pi-1/4Pi变化,喇叭后声波的相位变化是否也是一个对应渐变的过程.其中只有一点是最合适的,三,附箱体设计等效图,按这图管道长度应如何计算.谢谢.
再补充几点吧:
当KL<<1,a<<1时,Z[L]≈a=R-Ik△,Z[0]≈a-IkL,Z[0]和Z[L]同相,这即反相孔的低音增强效果。
当然也会出现一种情形:Z[0]和Z[-L]反相,也即Tanh[a-IKL]虚部为负。考虑KL>>a,即Tan[kL]<0,
这个对应于Pi/2<kL<Pi,此时会相消。
要是作为低频考量,箱内声压分布可近似认为是同相位的,改变相位的因素只是体积大小。对高频而言,
这个问题将显得比较复杂,这时不同形状会显著的改变箱体的等效阻抗,这里就不能把箱体看成纯粹的声容,
一旦箱体尺寸超过1/4波长,就有可能出现共振,这时比较有效的手段是尽量不要使箱体的相对面平行或者增加
阻尼材料。
至于管道长度的渐变和相位的变化从公式就可以看出来: Z[-L]=-Zr*I Tan[ (I a+k L)],只要声波频率和辐射
口尺寸不变,辐射声阻抗就不会变化,也即a不会变(注意a是虚数,有实部和虚部)。
楼上各位都是这块的高手,我只是试着就楼主所提问题做一个解释,这里可能会和实际情形不符合,还请指正。
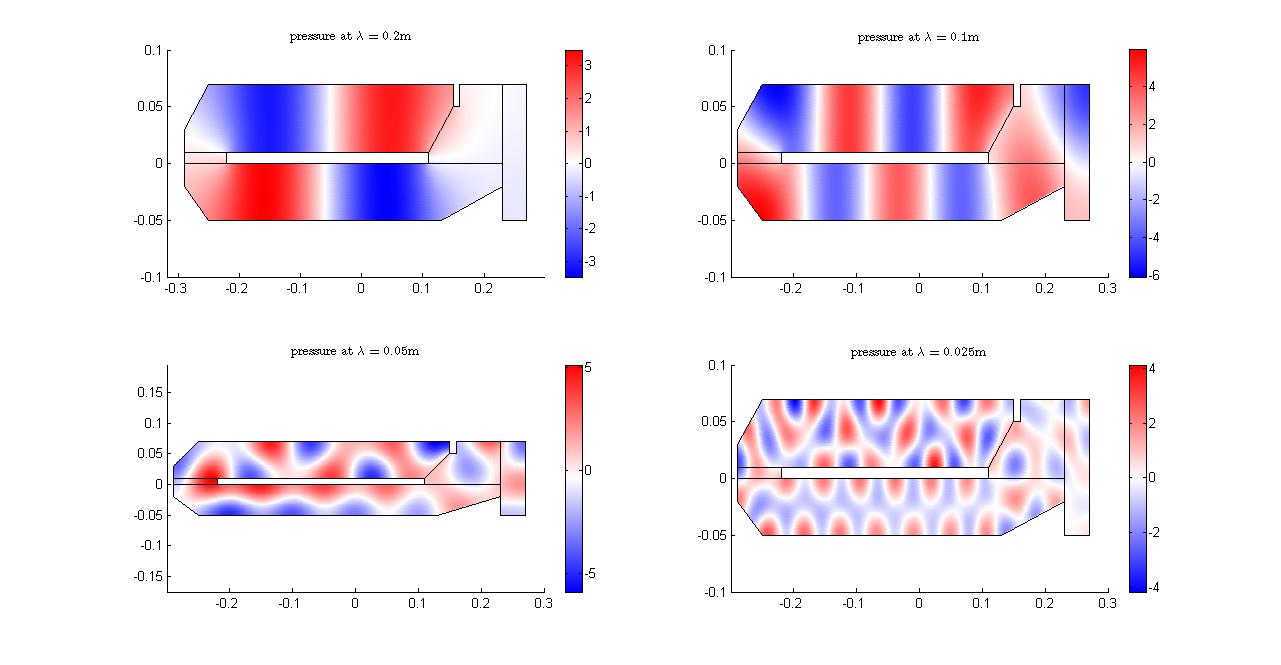
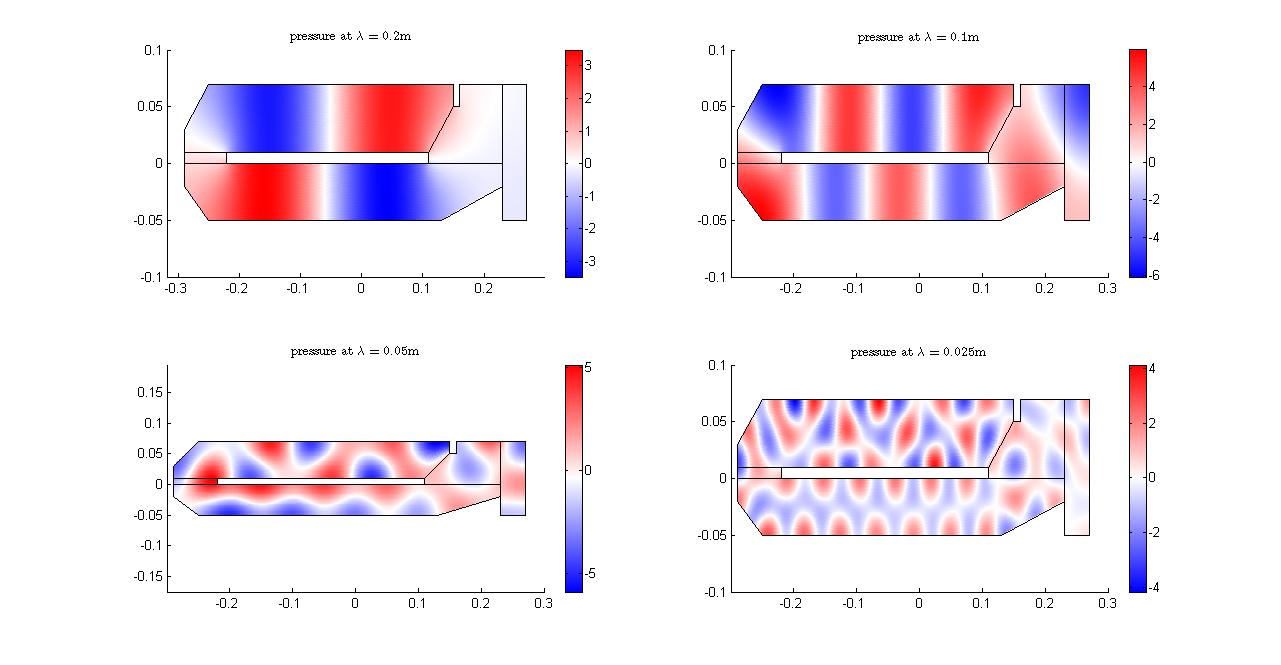
请问楼上的:这是怎样测出来的?
请多说一点点,谢谢了!
这可是很专业的“业余侠客”呀!望多指点。