共12 条记录, 每页显示 20 条, 页签:
[1]
[浏览完整版]
标题：倒相管的高级设计
1楼
huxueyou 发表于：2014-7-4 0:02:43我是做专业音箱的，大部分的专业音箱都是采用直线型倒相管。当然，在任何典籍上，为了计算方便，都是以直线型倒相管来讨论。
此主题相关图片如下：图片1.jpg
大家可以看到kr变小，R也变得越小了吗？kr就是周长除以波长的值了。对于倒相管，我们习惯性的分析圆形的，周长大，面积也就大了。
那今天我要和大家讨论更深层次的倒相管设计。也许我的思想，和前人在弧形倒相管上的研究有相同的结果。不过我还是要挖掘前人没有提出的观点。
在进行倒相管设计的时候，都忽略了倒相管的辐射面积。管面积只是在计算声质量的时候用到，而在辐射效率上，都没有去考虑过。这是本人要提出的话题。
大家分析号角的时候，常看到号角的下限频率和号角口的面积有关。这是为何呢？
事实上，声压的产生正如坛友上次讨论的时候提出的，和体积速度有关。也就是体积速度改变了空间的大气压强，产生了声压。
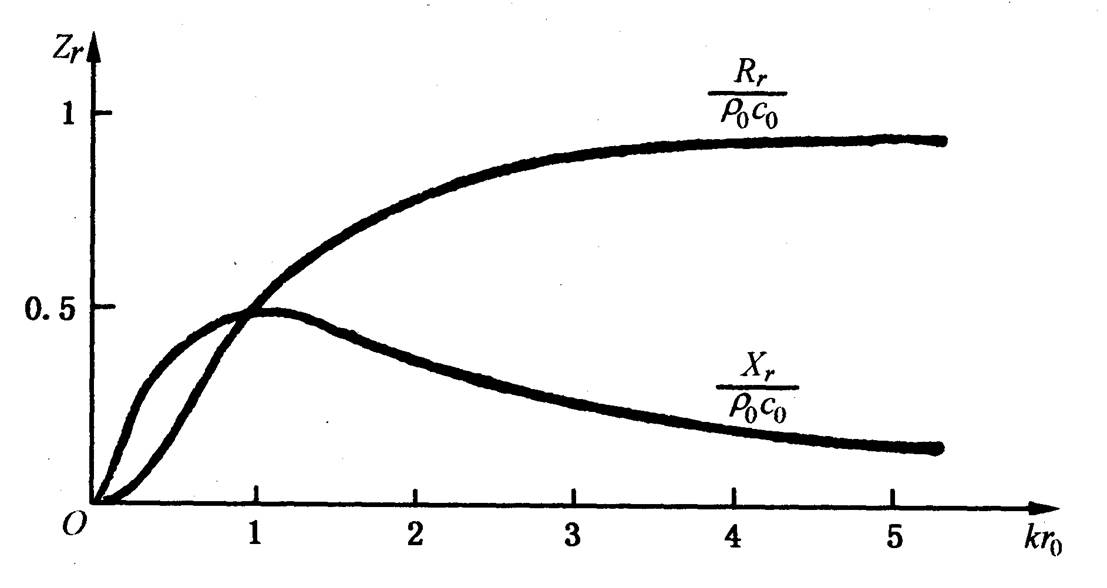
是不是体积速度会全部转变为声压呢？不会的，号角的分析过程可以搬来。体积速度转变声压的过程中，有一个阻抗问题，Z＝R+X。只有部分的R产生声声压，可另一部分R由于空气摩擦产生了热。而X是复数，它也没有产生声压。
R＝SρC（l/λ）^2/(（l/λ）^2+1) X=SρC（l/λ）/(（l/λ）^2+1) 仔细看，是不是有个参数不同？一个是二次方，一个是一次方？这个公式就是辐射阻抗公式。
此主题相关图片如下：图片1.jpg大家可以看到kr变小，R也变得越小了吗？kr就是周长除以波长的值了。对于倒相管，我们习惯性的分析圆形的，周长大，面积也就大了。
我们是不是可以得出一个结论，对于低频，虽然无法做到很高的辐射效率，但也是和面积有关？面积大，辐射的效率也会高呢？（不讨论谐振频点的原因）。
如果是这样，我们就很好解释了双曲线倒相管的原理，中间部位面积小，使得声质量变大，F0下降。而出口的面积大，提升了R，就是提升了辐射的效率，让低频很带劲？
所以我的看法就是，弧形倒相管，不仅是解决湍流的问题，而且还是一个阻抗变换器。加大出气口的面积，可使得低频下潜（F3）得更深，或是说可使低频的量更大。
具体能提升多少呢？如何量化呢？本人也推导出来一个运算式子。设周长增大X倍，那么声压增大的倍数是：
PX/P＝X^2*(（l/λ）^2+1)/(X^2*(l/λ）^2+1)
可能大家又看晕了，周长和波长都是动态的，这个公式怎么分析啊。没关系，我已经分析好了，当（l/λ）无穷小，LIM(PX/P)=X^2;(l/λ）有值但小于1时，LIM(PX/P)小于X^2,并大于1。就是说不管怎么样，都会有提升，最大的提升量是周长比的平方。
[此贴子已经被作者于2014-07-04 01:02:54编辑过]
2楼
dgtianxi 发表于：2014-7-4 9:17:42 这个结论有没有做实物试验过啊？
3楼
dgtianxi 发表于：2014-7-4 9:24:52我个人觉得作用不是太大，因为低频的波长很长，要想得到下限的提升，开口要做得很大才行。起码是波长的4分一长度以上。太大的尺寸在现实中没意义。只是个人的猜测，呵呵。希望楼主做实物验证一下。
4楼
玛田音箱 发表于：2014-7-4 17:42:15楼上正解，是真正把声学理论读透了人。
5楼
huxueyou 发表于：2014-7-5 3:02:52我认为可以形象一点理解吧。小管的质点速度快，碰上了管口相对静止的空气，它的损耗是不是大很多？大管的质点速度慢，损耗是不是小一点？
我测试过了，但我的测试工具不太理想。哪位朋友能测到低频？一直测测吧。
听感上，确实有改善，但不多。
6楼
dgtianxi 发表于：2014-7-5 9:12:37 这个不用测试仪器啊，你只要做两个箱子AB对比就可以了，如果你的观点是正确的，听感都能区别出来了。
7楼
huxueyou 发表于：2014-7-5 9:31:28对比过了，如果调到同样的FB，弯得比直的好。
8楼
huxueyou 发表于：2014-7-5 10:49:47从公式和图上可以看出，加大L，R是在上升阶段。具体说是多少，找个比方吧，直管是0.001，那弯管就是0.0015，还是比直管好了2DB啊。
9楼
卜凡 发表于：2014-7-17 13:24:01早都做过的了，在箱体厚度尺寸不够的情况下是可以把风管做成弯的的。
10楼
xiushuicunren 发表于：2014-7-19 8:52:36以下是引用huxueyou在2014-07-04 00:02:43的发言：
在进行倒相管设计的时候，都忽略了倒相管的辐射面积。管面积只是在计算声质量的时候用到，而在辐射效率上，都没有去考虑过。这是本人要提出的话题。
楼主的话好像不是很“全面”吧？
在一些稍微专业的书里都有关于倒相管辐射面积和倒相管开口形状的叙述的。
例如：当倒相管面积不够大的时候，会出现“非线性”和“功率压缩”等,也是行业里大家都注意了的问题。
至于开口是曲线，在现有的产品里是比比皆是吧？
这样的开口，要“像”号角一样的功能，因为频率很低（如50Hz），开口要多大才有明显的作用呢？
11楼
音行天下 发表于：2014-7-23 15:50:51学习下，谢谢
12楼
sailorflying 发表于：2015-9-3 16:48:54的确是有效果，但不能做的复杂。本人尝试用多个弯曲的管道组成的导向孔，但是发现结果并不理想。因为导向孔只是对于固定频率有作用，同时这个频率波长长，复杂了反而发生损耗。建议假如不是特别加强低音的音箱只是做前后的修正倒圆即可。
共12 条记录, 每页显示 20 条, 页签:
[1]